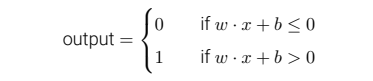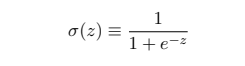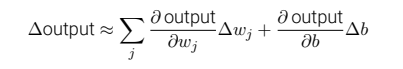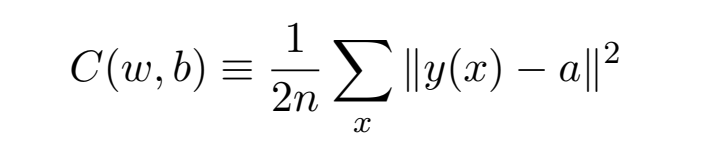本文阅读书籍与参考代码:
https://github.com/MichalDanielDobrzanski/DeepLearningPython
1 使⽤神经⽹络识别⼿写数字
神经⽹络使⽤样本来⾃动推断出识别⼿写数字的规则。另外,通过增加训练样本的数量,⽹络可以学到更多关于⼿写数字的知识,这样就能够提升⾃⾝的准确性。
1.1 感知器
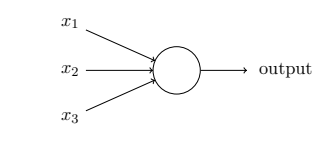
⼀个感知器接受⼏个⼆进制输⼊,x1, x2, . . .,并产⽣⼀个⼆进制输出。你可以将感知器看作依据权重来作出决定的设备。感知器的规则可以写为:
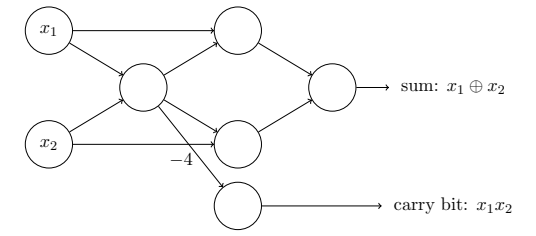
感知器网络可以表示为如下,并且我们完全能⽤感知器⽹络来计算任何逻辑功能,例如“与”,“或”和“与⾮”:
1.2 S型神经元
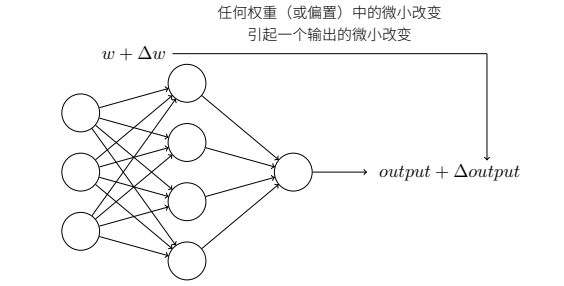
假设我们把⽹络中的权重(或者偏置)做些微⼩的改动。就像我们⻢上会看到的,这⼀属性会让学习变得可能:
如果对权重(或者偏置)的微⼩的改动真的能够仅仅引起输出的微⼩变化,那我们可以利⽤这⼀事实来修改权重和偏置,让我们的⽹络能够表现得像我们想要的那样。
例如,假设⽹络错误地把⼀个“9”的图像分类为“8”。我们能够计算出怎么对权重和偏置做些⼩的改动,这样⽹络能够接近于把图像分类为“9”。
然后我们要重复这个⼯作,反复改动权重和偏置来产⽣更好的输出。这时⽹络就在学习。
实际上,⽹络中单个感知器上⼀个权重或偏置的微⼩改动有时候会引起那个感知器的输出完全翻转,如 0 变到 1。因此,虽然你的“9”可能被正确分类,⽹络在其它图像上的⾏为很可能以⼀些很难控制的⽅式被完全改变。
我们引⼊⼀种称为 S 型神经元的新的⼈⼯神经元来克服这个问题。S 型神经元和感知器类似,但是被修改为权重和偏置的微⼩改动只引起输出的微⼩变化。这对于让神经元⽹络学习起来是很关键的。
S 型神经元有多个输⼊,x1, x2, . . .。但是这些输⼊可以取 0 和 1 中的任意值,⽽不仅仅是 0 或 1。例如,0.638 。
其中z ≡ w · x + b,σ 有时被称为逻辑函数。
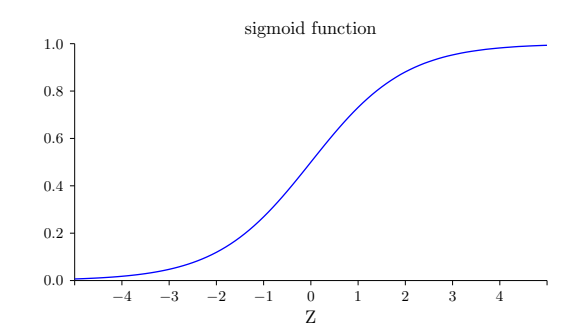
形状如下:
σ 函数的平滑特性,正是关键因素,⽽不是其细部形式。σ 的平滑意味着权重和偏置的微⼩变化,即 ∆wj 和 ∆b,会从神经元产⽣⼀个微⼩的输出变化 ∆output。实际上它的意思⾮常简单(这可是个好消息):∆output 是⼀个反映权重和偏置变化 —— 即 ∆wj 和 ∆b —— 的线性函数。这⼀线性使得选择权重和偏置的微⼩变化来达到输出的微⼩变化的运算变得容易。
S 型神经元不仅仅输出 0 或 1。它可以输出 0 和 1 之间的任何实数,所以诸如 0.173。
1.3 神经⽹络的架构
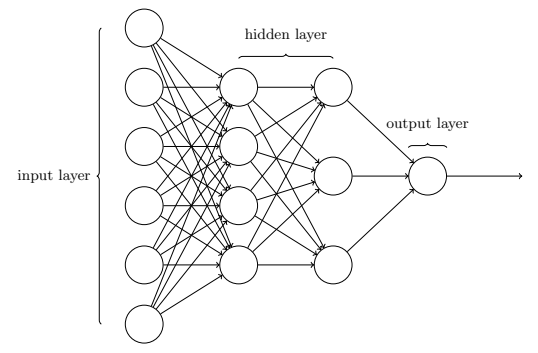
有这样一个网络:
这个⽹络中,最左边的称为输⼊层,其中的神经元称为输⼊神经元。
最右边的,即输出层,包含有输出神经元,在本例中,输出层只有⼀个神经元。
中间层,既然这层中的神经元既不是输⼊也不是输出,则被称为隐藏层。“隐藏”这⼀术语也许听上去有些神秘——但它实际上仅仅意味着“既⾮输⼊也⾮输出”。
1.3.1 网络层的设计
设计⽹络的输⼊输出层通常是⽐较直接的。例如,假设我们尝试确定⼀张⼿写数字的图像上是否写的是“9”。很⾃然地,我们可以将图⽚像素的强度进⾏编码作为输⼊神经元来设计⽹络。
如果图像是⼀个 64 × 64 的灰度图像,那么我们会需要 4096 = 64 × 64 个输⼊神经元,每个强度取 0 和 1 之间合适的值。
输出层只需要包含⼀个神经元,当输出值⼩于 0.5 时表⽰“输⼊图像不是⼀个 9”,⼤于 0.5 的值表⽰“输⼊图像是⼀个 9”。
⽬前为⽌,我们讨论的神经⽹络,都是以上⼀层的输出作为下⼀层的输⼊。这种⽹络被称为前馈神经⽹络。
1.4 ⼀个简单的分类⼿写数字的⽹络
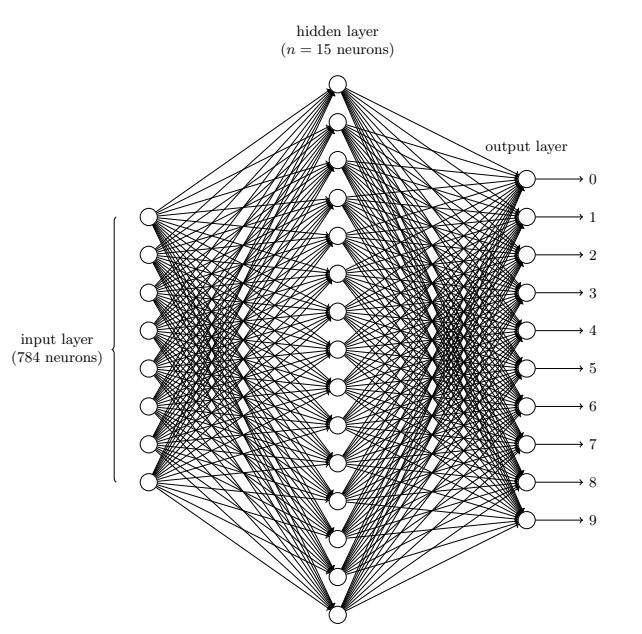
我们给⽹络的训练数据会有很多扫描得到的 28 × 28 的⼿写数字的图像组成,所有输⼊层包含有 784 = 28 × 28个神经元。输⼊像素是灰度级的,值为 0.0 表⽰⽩⾊,值为 1.0 表⽰⿊⾊,中间数值表⽰逐渐暗淡的灰⾊。
⽹络的第⼆层是⼀个隐藏层。我们⽤ n 来表⽰神经元的数量,我们将给 n 实验不同的数值。⽰例中⽤⼀个⼩的隐藏层来说明,仅仅包含 n = 15 个神经元。
⽹络的输出层包含有 10 个神经元。如果第⼀个神经元激活,即输出 ≈ 1,那么表明⽹络认为数字是⼀个 0。
1.4.1 隐藏层的神经元在做什么
假设隐藏层的第⼀个神经元只是⽤于检测如下的图像是否存在:
为了达到这个⽬的,它通过对此图像对应部分的像素赋予较⼤权重,对其它部分赋予较⼩的 权重。同理,我们可以假设隐藏层的第⼆,第三,第四个神经元是为检测下列图⽚是否存在:
这四幅图像组合在⼀起构成了前⾯显⽰的⼀⾏数字图像中的 0:
1.4.2 练习——十进制转二进制
通过在上述的三层神经⽹络加⼀个额外的⼀层就可以实现按位表⽰数字。额外的⼀层把原来的输出层转化为⼀个⼆进制表⽰,如下图所⽰。为新的输出层寻找⼀些合适的权重和偏置。假定原先的 3 层神经⽹络在第三层得到正确输出(即原来的输出层)的激活值⾄少是0.99,得到错误的输出的激活值⾄多是0.01。
| 原数字 | 二进制表示 |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
四位二进制用abcd表示,当十进制输入为8,9的时候,a=1。
所以可以设置权重为[0,0,0,0,0,0,0,0,1,1]T
例如,计算第一个神经元a的w·x,当第三层十进制输出8时:
- 激活值:当该位激活时=0.99,未激活时=0.01。第三层输出8时,8那个位置激活了,所以激活值=0.99
- 9的权重为1,但是未激活,所以激活值为0.01
- 计算
各位的权重·激活值并进行相加,结果=1.00
| 原数字 | 权重 | 激活值 | 计算w·激活值 |
|---|---|---|---|
| 0 | 0 | 0.01 | 0 |
| 1 | 0 | 0.01 | 0 |
| 2 | 0 | 0.01 | 0 |
| 3 | 0 | 0.01 | 0 |
| 4 | 0 | 0.01 | 0 |
| 5 | 0 | 0.01 | 0 |
| 6 | 0 | 0.01 | 0 |
| 7 | 0 | 0.01 | 0 |
| 8 | 1 | 0.99 | 0.99 |
| 9 | 1 | 0.01 | 0.01 |
| 1.00 |
又例如,计算第三个神经元c的w·x,当第三层十进制输出7时:
- 激活值:当该位激活时=0.99,未激活时=0.01。第三层输出7时,7那个位置激活了,所以激活值=0.99
- 2、3、6的权重为1,但是未激活,所以激活值为0.01
- 计算
各位的权重·激活值并进行相加,结果=1.02
| 原数字 | 权重 | 激活值 | 计算w·激活值 |
|---|---|---|---|
| 0 | 0 | 0.01 | 0 |
| 1 | 0 | 0.01 | 0 |
| 2 | 1 | 0.01 | 0.01 |
| 3 | 1 | 0.01 | 0.01 |
| 4 | 0 | 0.01 | 0 |
| 5 | 0 | 0.01 | 0 |
| 6 | 1 | 0.01 | 0.01 |
| 7 | 1 | 0.99 | 0.99 |
| 8 | 0 | 0.01 | 0 |
| 9 | 0 | 0.01 | 0 |
| 1.02 |
最后可以得出总表:
| 数字 | w·x(第一个神经元) | 第二个神经元 | 第三个神经元 | 第四个神经元 |
|---|---|---|---|---|
| 0 | 0.02 | 0.04 | 0.04 | 0.05 |
| 1 | 0.02 | 0.04 | 0.04 | 1.03 |
| 2 | 0.02 | 0.04 | 1.02 | 0.05 |
| 3 | 0.02 | 0.04 | 1.02 | 1.03 |
| 4 | 0.02 | 1.02 | 0.04 | 0.05 |
| 5 | 0.02 | 1.02 | 0.04 | 0.05 |
| 6 | 0.02 | 1.02 | 1.02 | 0.05 |
| 7 | 0.02 | 1.02 | 1.02 | 1.03 |
| 8 | 1.00 | 0.04 | 0.04 | 0.05 |
| 9 | 1.00 | 0.04 | 0.04 | 0.05 |
可以看出最大误差为0.05,那么我们可以设置偏置b为-0.06,就可以消去误差,然后规定至少大于0激活。比如,当第三层输出的数字为7,得出4个神经元adcd的输出w·x分别为[0.02,1.02,1.02,1.03],这时候去掉误差-0.06,得到[-0.04,0.96,0.96,0.97],-0.04未激活,结果=0。此时adcd=0111,也就是十进制的7。
1.5 使⽤梯度下降算法进⾏学习
把每个训练输⼊ x 看作⼀个 28 × 28 = 784维的向量。每个向量中的项⽬代表图像中单个像素的灰度值。我们⽤ y = y(x) 表⽰对应的期望输出,这⾥ y 是⼀个 10 维的向量。
我们希望有⼀个算法,能让我们找到权重和偏置,以⾄于⽹络的输出 y(x) 能够拟合所有的训练输⼊ x。为了量化我们如何实现这个⽬标,我们定义⼀个损失函数:
这⾥ w 表⽰所有的⽹络中权重的集合,b 是所有的偏置,n 是训练输⼊数据的个数,a 是表⽰当输⼊为 x 时输出的向量,求和则是在总的训练输⼊ x 上进⾏的。
我们训练算法的⽬的,是最⼩化权重和偏置的代价函数 C(w, b)。换句话说,我们想要找到⼀系列能让代价尽可能⼩的权重和偏置。
我们将采⽤称为梯度下降的算法来达到这个⽬的。
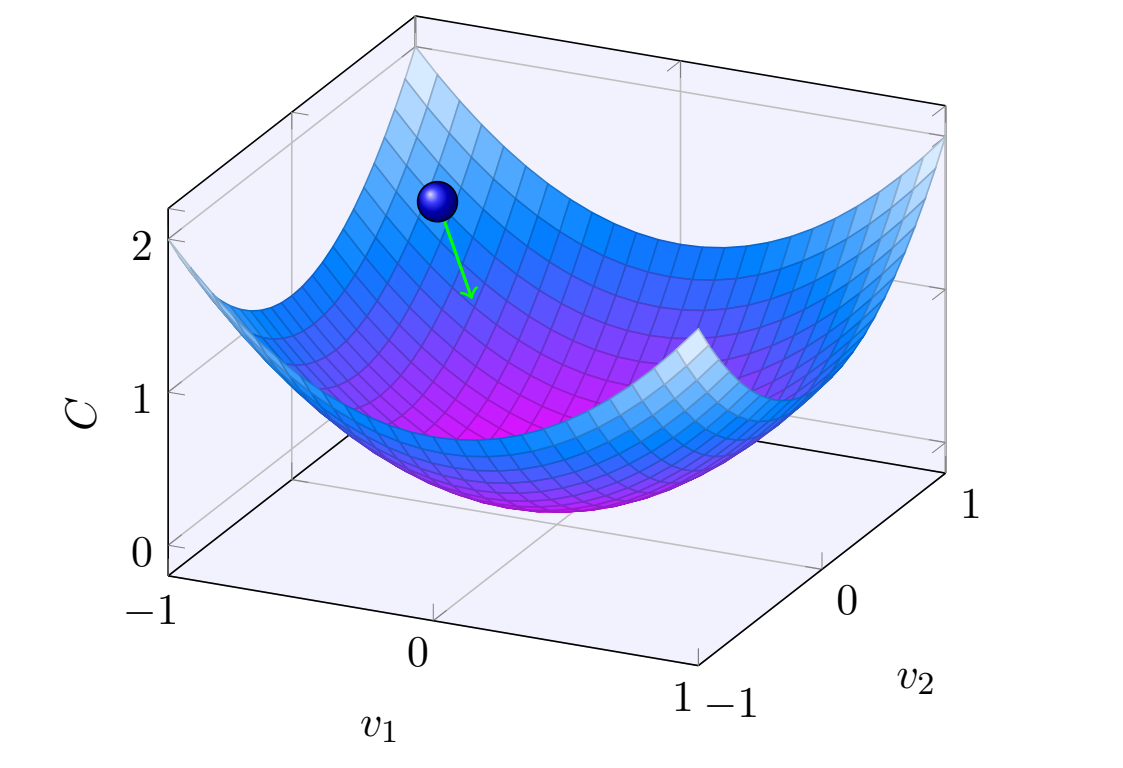
梯度下降算法⼯作的⽅式就是重复计算梯度 ∇C,然后沿着相反的⽅向移动,沿 着⼭⾕“滚落”。我们可以想象它像这样:
梯度下降法可以被视为⼀种在 C 下降最快的⽅向上做微⼩变化的⽅法。
1.6 实现我们的⽹络来分类数字
⼀旦我们给⼀个⽹络学会了⼀组好的权重集和偏置集,它能很容易地被移植到⽹络浏览器中以 Javascript 运⾏,或者如在移动设备上的本地应⽤。
建立一个test1.py文件,写入以下代码:
1import mnist_loader
2import network
3
4training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
5net = network.Network([784, 30, 10])
6net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
代码输出如下,最高准确率为95.08%:
1Epoch 0 : 8937 / 10000
2...
3Epoch 19 : 9508 / 10000
4...
5Epoch 29 : 9488 / 10000
将隐藏层神经元数量改到 100,准确率提升到了96%以上,⾄少在这种情况下,使⽤更多的隐藏神经元帮助我们得到了更好的结果。
当然,为了获得这些准确性,我不得不对训练的迭代期数量,⼩批量数据⼤⼩和学习速率η做特别的选择。正如我上⾯所提到的,这些在我们的神经⽹络中被称为超参数,以区别于通过我们的学习算法所学到的参数(权重和偏置)。如果我们选择了糟糕的超参数,我们会得到较差的结果。
.jpg)