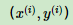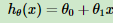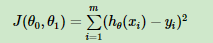参考：

https://zhuanlan.zhihu.com/p/49331510

https://zhuanlan.zhihu.com/p/24638007

https://zhuanlan.zhihu.com/p/357963858

https://www.cnblogs.com/pinard/p/5970503.html

1 SVM算法

支持向量机（Support Vector Machine，SVM）是一种经典的监督学习算法，用于解决二分类和多分类问题。其核心思想是通过在特征空间中找到一个最优的超平面来进行分类，并且间隔最大。

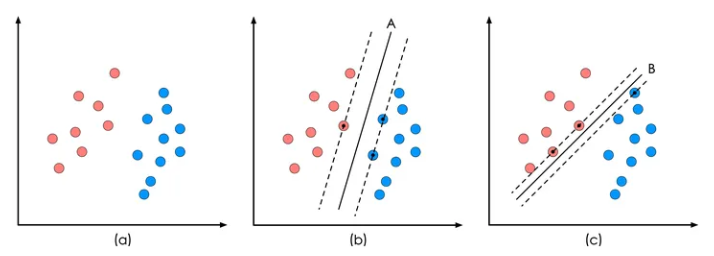
图1：

1.1 决策面

红色和蓝色的二维数据点显然是可以被一条直线分开的，在模式识别领域称为线性可分问题。然而将两类数据点分开的直线显然不止一条。(b)和(c)分别给出了A、B两种不同的分类方案，其中黑色实线为分界线，术语称为“决策面”。

1.2 分类间隔、支持向量

在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。

虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。

显然每一个可能把数据集正确分开的方向都有一个最优决策面，而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为“支持向量”。

对于图1中的数据，A决策面就是SVM寻找的最优解，而相应的三个位于虚线上的样本点在坐标系中对应的向量就叫做支持向量。

到这里，我们明确了SVM算法要解决的是一个最优分类器的设计问题。

2 随机梯度下降SGD

2.1 梯度下降法

大多数机器学习或者深度学习算法都涉及某种形式的优化。优化指的是改变 x 以最小化或最大化某个函数 f(x)的任务。

我们通常以最小化 f(x)指代大多数最优化问题。最大化可经由最小化算法最小化 -f(x)来实现。 我们把要最小化或最大化的函数称为目标函数或准则。当我们对其进行最小化时，我们也把它称为代价函数、损失函数或误差函数。

肯定有人问既然要最小化它，那求个导数，然后使得导数等于0求出不就好了吗？Emmmm…是的，有这样的解法，可以去了解正规方程组求解。但是那样的方式太难求解，然后在高维的时候，可能不可解，但机器学习或深度学习中，很多都是超高维的，所以也一般不用那种方法。

总之，梯度下降是另一种优化的不错方式，比直接求导好很多。

2.2 梯度方向

梯度的方向总是指向函数值增大的方向，即自变量沿着梯度的方向移动，函数值总是增大的。

梯度方向是上升方向，目标函数大多是loss函数，基本都是求最小值，那么就是就取梯度的负方向。

梯度下降的方向就是用负梯度方向为搜索方向，沿着梯度下降的方向求解极小值

在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。

可在数学上证明，此处不赘述。

2.3 梯度下降的直观解释

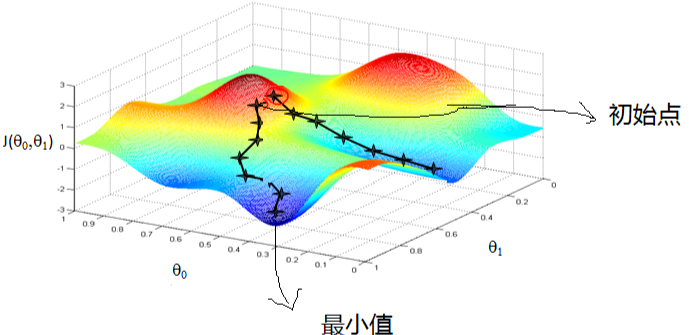
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

2.4 相关概念

步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
特征（feature）：指的是样本中输入部分，比如2个单特征的样本

，则第一个样本特征为x(0)，第一个样本输出为y(0)。
假设函数（hypothesis function）（拟合函数）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为hθ(x)。比如对于单个特征的m个样本

(i=1,2,…m)，可以采用拟合函数如下：

。
损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本（xi,yi）(i=1,2,…m)，采用线性回归，损失函数为：

其中xi表示第i个样本特征，yi表示第i个样本对应的输出，hθ(xi) 为假设函数。